


Next: The unitary equivalence of
Up: The non-equivalence of Weyl
Previous: Outline of the paper
The definition of a Majorana-neutrino field
For definitness I first discuss the quantitative definition
of a ``Majorana neutrino field''. In this I follow the standard
literature.
Let 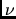 be a 4-component Dirac neurino field3Then, using ``east-coast'' notation (imaginary time)
the 2-component Weyl field
be a 4-component Dirac neurino field3Then, using ``east-coast'' notation (imaginary time)
the 2-component Weyl field 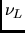 is defined4 as[1]:
is defined4 as[1]:
|
(1) |
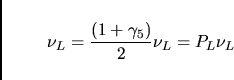 |
The
2-component Majorana field 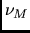 is defined via the following
relations by which the neutrino is its own antiparticle
[2]:
is defined via the following
relations by which the neutrino is its own antiparticle
[2]:
|
(2) |
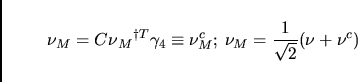 |
Here C is the charge conjugation matrix, 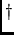 the
hermitian conjugate and T a transpose acting
only on the spinor,
the
hermitian conjugate and T a transpose acting
only on the spinor,
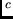 symbolizes charge conjugation and
a conventional ``creation phase factor''[3]
was set to 1
5.
The definition in eq.(2)
after the semicolon defines the field normalization and
it can be easily shown to
be the one that fulfills the usual
field-anticommutation axioms of quantum-field theory:
symbolizes charge conjugation and
a conventional ``creation phase factor''[3]
was set to 1
5.
The definition in eq.(2)
after the semicolon defines the field normalization and
it can be easily shown to
be the one that fulfills the usual
field-anticommutation axioms of quantum-field theory:
|
(3) |
![\begin{displaymath}
\left[ \nu_M(\vec{x},t),\eta(\vec{x}^{\prime},t) \right]_+=
i\delta(\vec{x}-\vec{x}^{\prime})
\end{displaymath}](img15.png) |
where 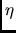 is the field which is canonical conjugate to
is the field which is canonical conjugate to
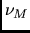 .
This field normalisation
(with the factor 1/
.
This field normalisation
(with the factor 1/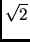 ) is generally used
in the literature[3,8,9,10,11]
6.
) is generally used
in the literature[3,8,9,10,11]
6.
Clearly the conditions eq.(1) and eq.(2) are
mathematically mutually exclusive; a Weyl particle can never be
its own antiparticle.



Next: The unitary equivalence of
Up: The non-equivalence of Weyl
Previous: Outline of the paper
Rainer Plaga
2001-08-03
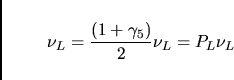
![\begin{displaymath}
\left[ \nu_M(\vec{x},t),\eta(\vec{x}^{\prime},t) \right]_+=
i\delta(\vec{x}-\vec{x}^{\prime})
\end{displaymath}](img15.png)