


Next: Proof that L L
Up: The non-equivalence of Weyl
Previous: The definition of a
The unitary equivalence of Weyl and Majorana neutrino
fields, also called ``Dirac-Majorana confusion theorem''
For the present argument it is
sufficient to consider
only charged currents in the low energy limit.
The standard-model (SM) Lagrangian for
massless Weyl neutrino fields is then:
|
(4) |
![\begin{displaymath}
L_{\rm Weyl}^{\rm SM}=
\bar{\nu}_L \gamma_{\mu} {\partial \o...
...left[W_{\mu}^- \bar{e}_L \gamma_{\mu} P_L \nu_L + H.C. \right]
\end{displaymath}](img17.png) |
here
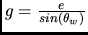 .
Let us now answer the following question: What Lagrangian
``
.
Let us now answer the following question: What Lagrangian
``
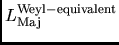 ''
must hold Majorana neutrino, so that it shows a phenomenology
identical to the one of the Weyl neutrino with Lagrangian (4)?
''
must hold Majorana neutrino, so that it shows a phenomenology
identical to the one of the Weyl neutrino with Lagrangian (4)?
Pauli[4] specified
the following ``Pauli I'' transformation ``U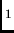 ''
which transforms a neutrino field
''
which transforms a neutrino field 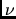 into
into 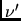 :
:
|
(5) |
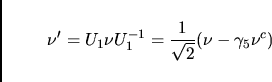 |
This transformation
7
can be easily shown to be unitary but does not
conserve a SU(2) invariance of a Lagrangian.
Similarity transformations leave
the form of operator
equations (i.e. in particular
the field equations and anticommutation
relations) unmodified and
the expectation values of field operators
do not change under a unitary transformation
of field operator together with
the field states[11,4].
Therefore the phenomenology remains unchanged
if one replaces 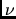 by
by 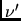 everywhere.
everywhere.
For the special case
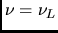 eq.(5) reads (h=helicity)8:
eq.(5) reads (h=helicity)8:
|
(6) |
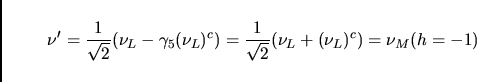 |
From the invariance of the field equations,
the Majorana Lagrangian is obtained by replacing
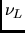 with
with 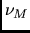 in equation (4)
in equation (4)
|
|
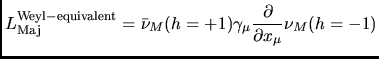 |
|
|
|
(7) |
![$\displaystyle + i g/\sqrt{2}
\left[ W_{\mu}^- \bar{e}_L \gamma_{\mu} P_L \nu_M(h=-1) + H.C.\right]$](img27.png) |
|
|
The ``Pauli I'' transformation
eq.(5)
does not include the electron field and is therefore
not equivalent to a mere representation change
of the theory. It is thus not at all clear if
this Lagrangian still obeys the standard model (see next section).
In the late 1950s (i.e. long before
the formulation of the standard model)
- with no reason whatsoever to
exclude the validity of L
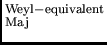 for
neutrinos - various authors
[13,14,15,16,17,18,19] could only conclude that
massless
for
neutrinos - various authors
[13,14,15,16,17,18,19] could only conclude that
massless 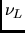 and
and 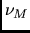 (helicity=
(helicity= 1 states) (and
analogously
1 states) (and
analogously 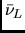 and
and 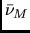 (helicity=+1 states)) are phenomenologically
completely equivalent
(this conclusion was later also called ``Dirac - Majorana confusion
theorem''[3]).
The ``Dirac - Majorana confusion
theorem'' was never discussed in the literature under the
assumption of quantitative validity of the standard model.
The difference between Majorana and Weyl neutrino is of a purely
quantitative character (a factor
(helicity=+1 states)) are phenomenologically
completely equivalent
(this conclusion was later also called ``Dirac - Majorana confusion
theorem''[3]).
The ``Dirac - Majorana confusion
theorem'' was never discussed in the literature under the
assumption of quantitative validity of the standard model.
The difference between Majorana and Weyl neutrino is of a purely
quantitative character (a factor 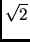 ) all qualitative properties
are the same (e.g. in the massless case both Majorana and Weyl neutrinos
conserve lepton number).
Kayser[3] and Zra
) all qualitative properties
are the same (e.g. in the massless case both Majorana and Weyl neutrinos
conserve lepton number).
Kayser[3] and Zra ek[20] state the confusion
theorem's validity
under the assumption that the weak interaction is left handed
(``qualitative validity'' of the standard model),
a correct statement which is not in contradiction with the present paper.
ek[20] state the confusion
theorem's validity
under the assumption that the weak interaction is left handed
(``qualitative validity'' of the standard model),
a correct statement which is not in contradiction with the present paper.



Next: Proof that L L
Up: The non-equivalence of Weyl
Previous: The definition of a
Rainer Plaga
2001-08-03
![\begin{displaymath}
L_{\rm Weyl}^{\rm SM}=
\bar{\nu}_L \gamma_{\mu} {\partial \o...
...left[W_{\mu}^- \bar{e}_L \gamma_{\mu} P_L \nu_L + H.C. \right]
\end{displaymath}](img17.png)