


Next: The definition of a
Up: Introduction
Previous: A remark about the
The review of the precise definition of the Majorana-neutrino
field in section 2 makes clear
that mathematically Weyl and Majorana fields are different.
Langrangians
predicted by the standard model for two mathematically different
fermion fields - even if they have the same degrees of freedom -
must not necessarily lead to the same phenomenology2.
Below I derive the Lagrangians giving rise to the same
phenomenology (briefly outlined in the
next paragraph ``1.'') and the Lagrangians derived
from the standard model (briefly outlined in
following paragraph ``2.'') and find
they are not identical.
1. In section 3
- as a review of work from several authors in the late 1950s -
it is shown that a unitary similarity
transformation (the ``Pauli I'' transformation)
between Weyl and Majorana neutrino fields exists.
One concludes that Weyl neutrinos with a standard-model (SM)
Lagrangian L
 can be unitarily transformed to a Majorana neutrino
with a Lagrangian L
can be unitarily transformed to a Majorana neutrino
with a Lagrangian L
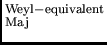 which is uniquely
specified by the condition that any similarity transformation
leaves the form of all field equations unmodified.
A Majorana neutrino obeying this Lagrangian is then
phenomenologically completely equivalent to a Weyl neutrino.
which is uniquely
specified by the condition that any similarity transformation
leaves the form of all field equations unmodified.
A Majorana neutrino obeying this Lagrangian is then
phenomenologically completely equivalent to a Weyl neutrino.
2. Since the late
1970s the interaction of the left-handed Weyl neutrino 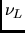 is uniquely specified by the standard model without
any reference to the observed
neutrino's properties,
(analogous to the top quark, whose weak-interaction properties were all
specified before its actual discovery).
Because a Majorana-neutrino field
can be decomposed to Weyl-neutrino components
via the ``Pauli I'' transformation, one
can derive the standard-model Lagrangian of a Majorana neutrino
L
is uniquely specified by the standard model without
any reference to the observed
neutrino's properties,
(analogous to the top quark, whose weak-interaction properties were all
specified before its actual discovery).
Because a Majorana-neutrino field
can be decomposed to Weyl-neutrino components
via the ``Pauli I'' transformation, one
can derive the standard-model Lagrangian of a Majorana neutrino
L
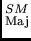 . One finds that L
. One finds that L
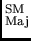
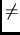 L
L
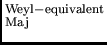 In other words:
the ``Pauli I'' transformation - that brings a Weyl to a
phenomenologically equivalent Majorana neutrino - is not
SU(2) invariant.
In other words:
the ``Pauli I'' transformation - that brings a Weyl to a
phenomenologically equivalent Majorana neutrino - is not
SU(2) invariant.
If the observed neutrino were
of Majorana type
it had to be phenomenologically equivalent to a Weyl
neutrino with standard-model interactions
to not contradict experimental facts (e.g.
about neutrino cross sections).
Under assumption A. in the introduction we can then conclude that the
observed neutrino must be of Weyl type.
The end of section 3 discusses why this conclusion
is not in contradiction with the pubished literature on the
``Majorana Dirac confusion theorem''.
Section 5 of the paper is devoted to showing in
detail how a Weyl neutrino with a Majorana mass term
can violate lepton number without ever being its own
anti particle and section 6 concludes.



Next: The definition of a
Up: Introduction
Previous: A remark about the
Rainer Plaga
2001-08-03