


Next: Summary
Up: The non-equivalence of Weyl
Previous: Proof that L L
Weyl neutrinos with Majorana masses
It could be that Lagrangian
(4) for a Weyl neutrino contains a small Majorana
mass term. In this section I first review the formal
reason why this leads to a lepton-number violating theory
and then analyze how this is possible for a particle
that is never its own antiparticle.
Lepton conservation is induced, according
Noether's theorem, by the invariance
of (4) under the following continuous
transformation group.
The charged lepton field e and
neutrino field 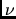 are simultaneously
transformed via[11]:
are simultaneously
transformed via[11]:
Considering
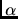 infinitesimal for the
infinitesimal field transformation
infinitesimal for the
infinitesimal field transformation
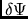 , Noether's theorem yields
lepton conservation.
The standard model Lagrangian
with the addition of a non standard-model
Majorana mass term
, Noether's theorem yields
lepton conservation.
The standard model Lagrangian
with the addition of a non standard-model
Majorana mass term 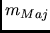 :
:
|
(12) |
![\begin{displaymath}
L_{\rm Weyl}^{\rm SM} =
\bar{\nu}_L \gamma_{\mu} {\partial \...
...right]
+ \left[ m_{Maj} {\bar{\nu}_L} (\nu_L)^c + H.C. \right]
\end{displaymath}](img45.png) |
The treatment of section 3 continues to hold.
This means:
1. Lagrangian eq.(12) is phenomenologically
equivalent to the Lagrangian
|
|
![$\displaystyle L_{\rm Maj}^{\rm Weyl-equivalent}=
\bar{\nu}_M
\gamma_{\mu} {\par...
... i g/\sqrt{2} \left[ W_{\mu}^- \bar{e}_L \gamma_{\mu} \nu_M(h=-1)
+ H.C.\right]$](img46.png) |
|
|
|
(13) |
![$\displaystyle + \left[ m_{Maj} \nu_M {\bar{\nu}_M} + H.C. \right]$](img47.png) |
|
|
2. assuming the validity of the standard-model
gauge sector the neutrino is definitely
not a Majorana field.
m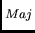 violates
the invariance of eq.(12) under the transformation
group eq.(11) because the Majorana mass term acquires
a phase of e
violates
the invariance of eq.(12) under the transformation
group eq.(11) because the Majorana mass term acquires
a phase of e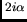 under
transformation (11).
under
transformation (11).
What is the mechnanism with which a Weyl field, which is
never its own charge conjugate, violates lepton number?
Consider the state of a Weyl field with a Majorana
mass in an inertial
frame at which it is a rest:
|
(14) |
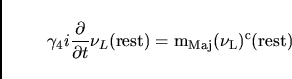 |
A solution to this equation in the Weyl representation is:
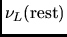 =
=
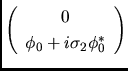 with
with
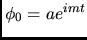 . This can be rewritten
as:
. This can be rewritten
as:
|
(15) |
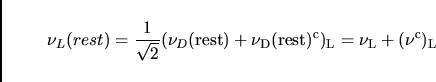 |
where
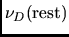 =
=
 describes a Dirac particle at rest.
This result means: in the rest frame
the Weyl spinor consists of the
components ``left-handed neutrino
describes a Dirac particle at rest.
This result means: in the rest frame
the Weyl spinor consists of the
components ``left-handed neutrino 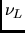 ''
(helicity =
''
(helicity =  1) and ``left-handed antineutrino
1) and ``left-handed antineutrino  ''
(helicity=+1) which are not
their respective charge conjugates.
A Lorentz boost along the z-axis can be shown to transform
''
(helicity=+1) which are not
their respective charge conjugates.
A Lorentz boost along the z-axis can be shown to transform
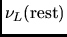 (with helicity=0) into a state
which is predominantly
(with helicity=0) into a state
which is predominantly 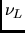 (helicity=
(helicity= 1)
or
1)
or  (helicity=+1). I.e. depending on the inertial
frame, a massive Weyl particle is predominantly particle
or antiparticle. In no frame it is its own antiparticle, however.
(helicity=+1). I.e. depending on the inertial
frame, a massive Weyl particle is predominantly particle
or antiparticle. In no frame it is its own antiparticle, however.
With a Majorana mass
term a Weyl field can thus violate lepton conservation,
without being its own antiparticle.



Next: Summary
Up: The non-equivalence of Weyl
Previous: Proof that L L
Rainer Plaga
2001-08-03
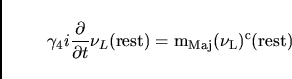
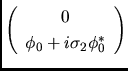 with
with
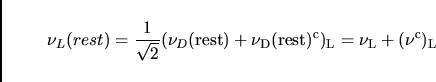
 describes a Dirac particle at rest.
This result means: in the rest frame
the Weyl spinor consists of the
components ``left-handed neutrino
describes a Dirac particle at rest.
This result means: in the rest frame
the Weyl spinor consists of the
components ``left-handed neutrino