


Next: Weyl neutrinos with Majorana
Up: The non-equivalence of Weyl
Previous: The unitary equivalence of
Proof that L
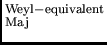
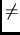 L
L
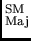
Let us calculate
the Lagrangian L
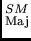 for massless Majorana neutrinos
that is predicted by the Standard model.
Applying P
for massless Majorana neutrinos
that is predicted by the Standard model.
Applying P onto eq.(6) one gets:
onto eq.(6) one gets:
|
(8) |
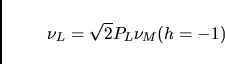 |
One can also show that [21,22]:
|
(9) |
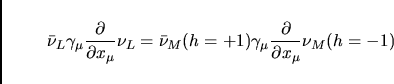 |
Replacing the kinetic term in Lagrangian (4) using
eq.(9) and 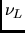 in the interaction term using
eq.(8) one gets:
in the interaction term using
eq.(8) one gets:
|
(10) |
![\begin{displaymath}
L_{\rm Maj}^{\rm SM}= \bar{\nu}_M(h=+1)
\gamma_{\mu} {\part...
...W_{\mu}^- \bar{e}_L \gamma_{\mu} P_L \nu_M(h=-1) + H.C.\right]
\end{displaymath}](img35.png) |
The charged-current coupling constant
in eq.(10) is seen to be a factor 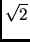 larger than
in eq.(7) the two Lagrangians are thus different.
larger than
in eq.(7) the two Lagrangians are thus different.
The numerical value
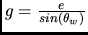 is determined in the standard-model
gauge theory by considering only neutral-current
(for
is determined in the standard-model
gauge theory by considering only neutral-current
(for 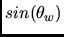 )
and electromagnetic (for
)
and electromagnetic (for 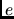 )
reactions of the electron, i.e. without reference to
neutrino properties.
One numerically different coupling constant
in the two otherwise identical Lagrangians eq.(7) and
eq.(10)
is a difference which persists
to the phenomenological level (i.e.
the application of Feynman rules). In other words:
if the neutrino is a Majorana particle and its gauge
interactions are the one of the standard model, charged-current
reactions of the neutrino would have a factor 2 larger
cross section than observed.
If we assume the strict validity of the
standard model gauge sector
a priori (see assumption A
in the introduction)
the observed neutrino, if massless must be a Weyl
neutrino, i.e. definitely not its own antiparticle.
This conclusion rests only on the
quantitative consideration of the
charged current ``source'' term
)
reactions of the electron, i.e. without reference to
neutrino properties.
One numerically different coupling constant
in the two otherwise identical Lagrangians eq.(7) and
eq.(10)
is a difference which persists
to the phenomenological level (i.e.
the application of Feynman rules). In other words:
if the neutrino is a Majorana particle and its gauge
interactions are the one of the standard model, charged-current
reactions of the neutrino would have a factor 2 larger
cross section than observed.
If we assume the strict validity of the
standard model gauge sector
a priori (see assumption A
in the introduction)
the observed neutrino, if massless must be a Weyl
neutrino, i.e. definitely not its own antiparticle.
This conclusion rests only on the
quantitative consideration of the
charged current ``source'' term
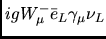 ;
as long as only kinetic, mass and the form
of the interaction term are considered
(as is done in all
equivalence proofs in the literature!)
Majorana and Weyl fields are seen to be completely equivalent.
;
as long as only kinetic, mass and the form
of the interaction term are considered
(as is done in all
equivalence proofs in the literature!)
Majorana and Weyl fields are seen to be completely equivalent.



Next: Weyl neutrinos with Majorana
Up: The non-equivalence of Weyl
Previous: The unitary equivalence of
Rainer Plaga
2001-08-03