- ... R.Plaga1
- plaga@mppmu.mpg.de, see http://hegra1.mppmu.mpg.de/majorana for
additional material on this manuscript
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... phenomenology2
-
An example where this is obvious is e.g. a Weyl neutrino and
a massless electron.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... field3
-
I do not discuss the possible
case of Dirac neutrino masses in this paper.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... defined4
-
I do not explicitely include the condition of fermion number
conservation in this definition, as is sometimes
done in the literature.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... 15
-
This defining constraint for Majorana fields (``Majorana neutrinos
are eigenstates of C'')
is universally accepted
in the literature, also
after the discovery of parity violation (e.g. eq.(19)
in Pauli's paper[4] written after the
discovery of parity violation, or e.g. eq.(10) in
Ref.[5]). Even if one
prefers Kayser's alternative characterization of
Majorana neutrino as a state that
is turned into itself with reversed helicity under CPT
[3], eq.(2) has
to hold.
E.g. in a textbook by Mohapatra and Pal
[6] the CPT properties of Majorana
neutrinos are derived in section 4.4.3 using
their eq.(4.16) which is identical to eq.(2).
Berestetskii et al.[7] argue that
there is no problem with condition (2)
even in the presence of weak interactions
because it is invariant not only to
CPT but also with respect to each
of these transformations seperately.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...kayb,mannheim,fukugita,lee,roman2
6
- Only Bilenky and Petcov[12] leave the
factor 1/
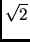 out, for reasons that are not clear
(they quote Ref.[8] that does use it
as standard reference for the definition of a Majorana
fermion.)
out, for reasons that are not clear
(they quote Ref.[8] that does use it
as standard reference for the definition of a Majorana
fermion.)
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... transformation7
- The explicit form
of U
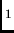 can be found in
Refs.[13,9]
can be found in
Refs.[13,9]
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... (h=helicity)8
- The Pauli I
transformation of
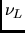 is
is
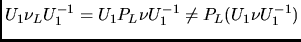
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.